Condition monitoring: performance
A topological method for NPP optimisation
20 September 2011The computer-based analysis of thousands of nuclear power plant parameters gathered in near real-time can improve nuclear power plant efficiency by flagging up novel links between parameters. By Massimo Teglia, Mario Zadra, Annalisa Perasso and Francesco Benvenuto
Since the performance of a nuclear power plant is mainly bound to the conversion of thermal to electrical power, improvement in knowledge of the thermal cycle and electrical generation behaviour would improve global plant performance.
The conversion of thermal to electrical power through a water/steam thermal cycle today represents the most convenient method to obtain usable energy from a nuclear reaction at a large scale. That thermal cycle consists of a complex succession of thermohydraulic transfer operations working in a closed loop. Traditionally each operation is finely tuned with sophisticated regulation devices that provide correction based on the behaviour of a few input parameters to maintain the level of the selected parameter’s output close to the predefined set point.
Each loop in the chain is regulated to stabilize its output independent of the stability of the input. Conceptually speaking, the entire system is searching for stability.
Since electrical power is the end product of the thermal cycle, it should be considered as the sole variable (the target parameter); all other parameters may be kept at their predefined set points. Two qualifications should be made to such a scenario:
- In reality the entire system is not so simple; the environment surrounding the thermal/electrical conversion process is continuously changing
- Regulation of each loop of the chain does not have an instantaneous effect. The feedback delay reduces the stability of the regulated output.
As a consequence the cycle is affected either by external perturbations or by perturbations produced by delayed response in each feedback loop.
External perturbations trigger variation in the feedback loops. Feedback delay does not allow immediate perturbations to be smoothed out. Consequently, the original perturbation induces a chain of secondary perturbations that affect the entire cycle.
Sometimes the perturbation is smoothed within the cycle; sometimes it goes beyond that cycle to affect the next step; sometimes the perturbation travels through all of the steps in the cycle until it reaches itself, producing a static effect. Many such effects with different frequencies could exist at the same time in the cycle.
From this introductory description of a very complex system of overlapped effects two different considerations emerge:
- Could a hypothetical ‘regulator of the regulators’ improve performance through better stability of electrical power output?
- Could the electrical power output level be affected by underlying effects which up until now have not been considered to be aspects that can be improved?
To obtain the answers to the above questions an analysis method has been developed to define a general algorithm capable of identifying and clustering each perturbation affecting electric power output trends.
The developed method works like a simulation of the plant using the plant historical data as an input.
The proposed theory is currently being tested at two nuclear power plants. Once confirmed by analysis and by field results, that is, the extent of recoverable electrical power, the authors’ intentions are to develop an automatic plant supervisor. This supervisor would be capable of working methodically 24 hours a day for the lifetime of the plant, learning from the past to automatically provide settings for plant feedback loops.
Data processing
Plant performance monitoring is still considered as an engineering activity to be carried out manually with limited automatic support. Although a plant’s automatic data processing system generates and stores a lot of plant process data, these data are normally dedicated to the direct process control.
However, if the plant automation system could directly and automatically feed plant process data to an information database, and these data could be automatically processed, they would create a global plant performance analysis.
Results of an automatic performance analysis cover:
- Performance shortfall identification
- Early failure identification
- Design parameter validation
- Process parameter tuning
- Plant behaviour modeling
- Component ageing integration and accounting
- Prioritization of maintenance activity
- Overall plant status, provided in real time.
Development of the project consists of three different steps:
a) Preparation of the reference database and the automatic feeding structure
b) Development of the analysis tools and interfaces
c) Development of the real-time data processing engine.
Plants usually record all process parameters using an electronic format with a sampling frequency from 0.2 Hz for the oldest plant to 2-5 Hz for the modern ones. The format of the stored data is very simple: time, parameter name and value. Since a plant has from 1000 to 5000 recorded parameters, these data represent a huge amount of available information. The only data required are recorded process data, and information about maintenance activities performed.
Conceptually, the recorded information represents a complete description of the plant ‘universe’. Variations in the values of the parameters describe plant evolution. A prolonged and in-depth analysis of the variations in parameters and the relationships among them allows us to obtain a complete written picture of the plant’s status and evolution.
If the available information set is complete, then theoretically the plant status at the next instant is perfectly foreseeable, with a certain amount of error. That error is due only to parameters external to the plant, which are not perfectly foreseeable.
Data received from the plant are processed to obtain information in a useful form. A database is required to correctly process the data. In that database are coded the following data:
- Instruments and information sources catalogue, including the precision class of each instrument and quality class assignment rules (the quality class concept is discussed below)
- Equipment and lines catalogue
- Process flow structure, with its relation to equipment, lines and instruments
- Operating conditions and target parameter definitions
- Symmetry and congruency catalogue (describing equipment and lines with similar process conditions)
- Target structure definitions. Because it is not practicable to define the exact relationship of each one of thousands of parameters to electrical power output, a hierarchy of targets has been created. The analysis is repeated for each of the targets included in the cluster. For example, the level of a feedwater heater is linked to feedwater temperature, which is an intermediate target. Level of the heater influences the feedwater temperature, which affects electrical power output).
A quality class represents a slice of values for a certain parameter [Figure 1]. The entire range of values of each parameter is divided in a predetermined number of slices (usually between 99 to 9999), including some additional ranges. Each slice is called a quality class. Normally the quality class corresponding to the nominal value is set in the middle of the scale, meaning quality class 500. Parameter trends are analyzed using quality classes instead of values to cancel the noise of the original signal.
The philosophy of the proposed system is to provide plant information in a different form from the traditional time/parameter/ value. To do so requires a pre-processing activity carried out by predefined algorithms whose goal is to offer a different point of view without affecting the information. Data fed from the plant is processed in two different ways: achronological and chronological.
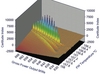
In the first case, achronological, the values are processed in order to obtain numerical correlations between each single value and that of the target parameter [Figure 8].
The second case, chronological, is divided in two sections: configurations and events.
By assigning a quality class code to each parameter value, it is possible to record the entire plant configuration for each processed instant. The data are collected into a single file indicated by an unequivocal key. They refer to the main target parameter for that instant (usually the plant power output).
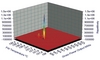
An event is opened for each parameter quality class that has been changed from the previous instant. An event is unequivocally identified by the parameter name and the time when it is started. An event is closed when the parameter value returns to the quality class corresponding to its nominal value. For each event, significant information is collected: duration, amplitude (in quality class), time since the previous event, and so on. An example of the event frequency analysis is shown in Figure 2.
Configurations and events are calculated based on real data and on estimated data. The next value automatic calculation uses neural computation to provide the value of each parameter expected at the next instant. The neural network computation allows the building of transfer functions on a heuristic basis. It considers a certain parameter’s historical trend as one input, and the related timeline as another input. Then the neural network is capable of recreating the mathematical law that drives the trend. Likewise, by providing a time value beyond the previous window, the neural network can estimate the corresponding parameter value. The greater the history available, the better the precision of the estimation. The process obtains an estimated value range as a result of a double calculation process:
- Estimation based on the historical trends of the processed parameter
- Estimation based on the behaviour of all parameters excluding the processed one.
The first process predicts the next chronological value, based on the parameter’s historical trend. The second process analyzes the expected value of the parameter considering the values of all the other parameters within the same window of time. The database of knowledge required for second process is obtained through the observation of entire population of variables. The influences produced by every other parameter on the one under analysis are recorded. In this way, the second process is able to predict the expected value of each parameter based on the behaviour of all other parameters.
Although the processing of the next instant estimated value in configurations is carried out in the same way as for the real value, the processing of events for estimated values is different from that of real values. An event is begun for next instant estimates once the quality class of the expected data results differ from what happened. That allows us to obtain an early alert of potential failures.
The final factor in the chronological global plant performance monitoring process is an estimate of feedback delay. The set of values for each instant contains information about the plant parameter trends, but the information is still not correctly aligned on the time axis. The lack of proper temporal alignment makes any data obtained so far by this method indefinite. In fact, the propagation of an effect through multiple processed parameters is not instantaneous. Each target parameter suffers a different delay in its variation depending on the parameter that produced the variation; the difference is a time constant [Figure 3]. The time constant is automatically computed based on event trends, and a correction is then applied to the input data. This procedure allows us to obtain all chronologically-processed input values in a perfectly-aligned temporal sequence. This alignment allows a determination of cause and effect on the basis that the causes occur before the effects.
The claim that the plant universe and its evolution are comprehensively represented by the values of the gathered parameters requires further support. For example, it is possible for a single configuration to produce different values of the parameter target. This phenomena indicates that in the plant universe something affecting the target remains uncontrolled. This information represents an important tool in order to hunt the uncontrolled variables that affect the plant performance. Since all the design parameters are submitted for control, the evidence that some uncontrolled variables exist leads to two different explanations:
- Initial design considerations were incomplete
- An external environmental variable or a human factor is affecting plant performance.
In order to manage those cases, the process analyzes each level of power output using the unequivocal code of each configuration in order to list the different configurations present for each level of power output. (For each value of the target parameter, multiple plant configurations could exist; these plant configurations are a combination of different quality classes of the parameters). Comparison of the variation between different parameters in different configurations that result in the same level of power output allows one to exclude parameter variation that has no effect.
Figure 4 displays a schematic view of plant configurations, and how they are created. The entire plant is represented by all the collected parameters (variables). The entire set of parameters is a vector of values where the first parameter of the vector is generically called ‘I’ and the last ‘N’. ‘Pout’ is the parameter that represents the level of power output of the plant. Each variable is assigned a quality class. Every configuration has its own unequivocal code. Also shown in the diagram is the power output step, which shows the ‘Pout’ obtained with the combination of parameter values that are reported within the matrix beneath as quality classes. ‘Repetition number’ represents the number of times that the same configuration produces the same level of power output.
The method is referred to as topological because much of the analysis is geometrical in nature. From a mathematical point of view, the matrix of values that represents a configuration is converted into an equivalent geometrical form. There is more or less one form for each section of the process. The obtained forms are analyzed from a geometrical point of view. Different forms of the entire cycle should match each other perfectly. In cases of divergences, the points of interference between the forms represent anomalies. A point of interference can be easily brought back to the involved variables. That method is an application of geometrical topology and it has been adopted to speed up the huge amount of computation required by the methodology.
Time coding
A coding format for time description has been introduced to have a unequivocal description of the time of each instant experienced by the plant, starting from the plant commissioning and finishing at the end of its extended life. This coding [Figure 5] includes various levels of time description: lifetime (original or extended plant life), year, season, month, week, day of week, shift, hour, minute and second. The time levels are also considered to be inputs. They allow us to associate events with a certain time condition (for example, certain days of the week, season or shift). In this way the number of uncontrolled variables is reduced.
Time coding also enables an additional data processing step. Data originally received on a high-frequency basis (in seconds or fractions) reports its average value (obtained through a dedicated statistical algorithm) to the next higher time level. This values reporting process is performed at all the levels considered. The entire process described in the present paper is simultaneously carried out in 12 different levels of time; so there is a process carried out each five-second period, each 15-second period, each minute, and so on.
Extrapolating from the data in this way can be useful. Providing a path for the expected trend of the lower-level information permits an extension of the function describing the path of a foreseen value to the point where it diverges from the real value [Figure 6]. Trends found at an upper level (for example a frequency of 15 seconds) represent a kind of channel; the immediately lower trend (for example a frequency of 5 seconds) should remain within that channel. Cases of divergence are considered abnormalities. If, for example, the method detects a deviation of 1.2 mm/year in a generic vibration measurement, then a deviation of 0.1 mm would be expected on a monthly level. If the deviation went beyond that figure, it would be flagged as an anomaly. Used over long time scales (months and years), this approach could define factors such as seasonability and aging.
Goals
The purpose of the described data processing method is to obtain perspectives of plant status that cannot be reachable using traditional methodology. The method produces several projections of the same value. Moreover, the reading time of each measurement is updated using the time correction. To be able to recognize the original value/time pair at any moment, they are specially marked. Taken together, these data represent a continuously updated status of the plant, which can be further analyzed by tools and interfaces. These tools, directly connected to the databases, allow the definition of:
- The best performance point for each parameter depending on its target [see Figure 7]. This evaluation is performed achronologically. By using real conditions found in the plant, we can obtain the optimum working point even if it is out of the processed values range, by using analytical and neural computation
- Early event alerts, obtained from a ‘next value’ calculation based on previous trends. Discrepancies between the expected and real value highlight abnormal conditions, which are useful as early warning of failures. The ‘next value’ calculation is obtained through a double neural computation: the first on the time line basis and the second one based on the expected value within a certain parameter values set
- Heuristic models based on modelling hypothetical process conditions, and which can be used to predict plant responses [see Figure 8]. The configuration database associated with the achronological process allows us to predict plant response in operational conditions not previously tested
- Aging evaluation, preventive maintenance requirements and equipment performance losses of particular systems can be reached by a long-term deviation analysis of their parameters' effect on their target, including the history of work performed by related equipment and components.
Results
Although this entire methodology is still under development, some confirmatory results have already been obtained from studies of a combined total of four years of operational data from two nuclear power plants: one in Europe, one outside of Europe. First, it was found that the method can validate designed nominal values of process parameters. From a numerical point of view, each nominal value (one for each parameter of the plant) is the result of a transfer function. The method considers all the plant parameters as input of the transfer function, excepting the parameter under analysis that it represents the output of the function. In case the result of the function differs from the originally designed nominal value, input parameters are replaced one by one by the originally designed nominal value and the function reprocessed. The process is iterated until all the unaligned nominal values are found. This method highlights the nominal values that have been not correctly designed. Furthermore, for each unaligned nominal value, the root causes of the misalignment are evident.
Second, the introduction of the correction of the recorded parameters’ chronology permitted us to exactly define the cause/effect mechanisms between the collected values. A comparison of thermal power output and electrical power output using the relative time correction demonstrates that the designed and actual values are not aligned [Figure 9]. In fact, the designed electrical output is obtained with a lower actual thermal power than was designed. Also, at the designed thermal power the corresponding actual electrical output is lower than was designed.
A distribution chart of thermal power output level [Figure 10] shows that the plant runs only relatively infrequently at the nominal thermal power value taken from Fig. 9, indicated as the best performance point. Most of the time, the plant is working closely to the original nominal thermal power output, which was shown to be less efficient in Fig. 9. These results confirm that the proposed method can optimize the two most important plant parameters, thermal and electrical power output.
Other secondary results have been obtained. Turbine bypass valve leaks were detected through the event analysis; the process found a similarity between the small variations in the main condenser pressure and minor variations in the position transmitter of one main steam bypass valve. The method also highlighted abnormal ageing in main generator stator coils.
The process can provide general plant tuning, improving the operating conditions and producing economic benefits.
The proposed methodology envisages the possibility to define and validate two sets of nominal values; one for a specific plant design, and one calibrated for each plant. The chance to have a specific nominal value set for each plant gives the opportunity to balance the differences between plants with the same design. The aim is to obtain plant performances closer to the original design target.
Future aims include improving the methodology, and the computational capability by adopting supercomputing. These improvements will be applied in two ways: first, as a plant assistant that works in real time; second, integration with the database that supports probabilistic risk assessment. The latter will be covered in a future paper.
Author Info:
Massimo Teglia, project manager, Mario Zadra, senior mechanical & process engineer, Francesco Benvenuto, process engineering manager, Ansaldo Nucleare S.p.A., c.so Perrone, 25 - 16161 Genoa, Italy. Annalisa Perasso, PhD Mathematics, University of Genoa, Via Balbi, 5 - 16126 Genoa, Italy. A version of this paper was presented at the Power Russia 2011 conference and exhibition, 28-30 March 2011, Moscow.