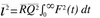Testing fission chambers

The measurement of neutron flux is important for all nuclear reactors because it can be used to predict reactor thermal power. Fission chambers are often used for this purpose in pulse and mean square voltage (Campbell) modes enabling neutron flux to be monitored from reactor shut-down to full power using a single chamber. Fission chambers used for safety-critical reactor protection require routine testing. Analysis of the Campbell signal can provide important information about the condition of a fission chamber. However, such analyses are not usually carried out during routine testing. A new piece of equipment—the signal analyser—has been developed for this purpose.

Fission chamber operating modes

Fission chambers consist of a pair of electrodes, one of which is coated with a fissile material, which is usually uranium-235. The space between the electrodes is filled with inert gas, which is often argon with a small percentage (4%) of nitrogen. When a neutron interacts with a U-235 atom, fission occurs, resulting in an ionized track through the fill gas. A polarising voltage between the plates prevents the ions and electrons from recombining. Electrons travel towards the anode and positive ions drift towards the cathode, producing a pulse of current. Ionisation tracks at different angles produce different pulse shapes. Each neutron that causes a fission in the chamber produces a pulse of current. These pulses are detected and converted to a pulse count rate. All the individual pulses occurring randomly in time add together. As neutron flux and hence pulse-rate increases, pulse pile-up occurs when pulses start to coincide in time, and are counted as one by the electronics. This usually starts to occur at 500,000 counts/sec or so, depending upon the collection-time and the pulse-shaping used in the electronics.

Fission chambers can be used in three different operating modes. For the measurement of low neutron flux levels the pulse counting mode is used (about 100-1x108 nv (neutrons per centimetre squared per second), with a sensitivity of 0.01 counts/second/nv, for the Photonis CFUM21 in-core fission chamber as an example). The presence of nitrogen in the fission chamber increases the electron velocity. A higher electron velocity results in a shorter collection time when used in pulse mode. This allows pulse mode to be used at higher pulse rates than would otherwise be possible, without excessive counting losses through pulse pile-up.

At high neutron flux levels (1x10⁸-1x10¹² nv for the Photonis CFUM21) the chamber can be used in the DC mode. The individual pulses combine to give an average DC current that can be used to give an indication of the neutron flux. However, the current from the chamber will also show random fluctuations. These fluctuations can also be used as a measure of the neutron flux (in the range 1x10⁶-3x10¹¹ nv for the Photonis CFUM21). This third operating mode is known as Mean Square Voltage (MSV) mode or Campbell mode after N. R. Campbell who developed the mathematical theorem [1].

The Campbell measurement principle is based upon the mathematics of random events. When the neutron flux is beyond the upper limit of pulse counting, the output of a fission chamber consists of a fluctuating DC current. The fluctuation is related to the neutron detection rate by the following formula (Equation 1):

Equation 1

Where:

i² is the mean square detector current

R is the mean neutron detection rate

Q² is the mean square charge per detection

F(t) is the response of the electronics to one pulse

This means that the mean of the square of the current is proportional to the neutron flux. This is usually stated in papers relating to the use of Campbell’s theorem for neutron flux measurements. What is often not made clear is that this is actually a simplification. There is more information in the signal than Equation 1 implies, as will be explained later.

Often, the pulse counting and Campbell modes are combined in one instrument to cover typically ten decades of neutron flux measurement with a single detector [2]. A significant advantage of the Campbell measuring mode over DC mode is that it has an inherent ability to reject small pulses, such as those induced by gamma photons. This is because the final result is proportional to the square of the charge per event. Typically, the gamma contribution is two decades less than in DC mode [3]. Combined pulse/Campbell instruments are used on many types of fission reactor. A combined pulse/Campbell instrument can replace more conventional systems where two or three different detectors are used to cover the full range, or can be used as a diverse measurement technique [4]. The use of diverse measurement techniques improves confidence in the measurements and assists with setting up the instrumentation [5].

A new Campbell mode signal analyser has been developed that can be used to test newly-manufactured chambers, periodically test stored spare chambers or to test chambers that are installed in a reactor for safety protection.

The Campbell spectrum

In the Campbell mode pulses caused by fission events combine to produce a continuous spectrum. However, it is important to understand that this spectrum is not flat. The electrons travel very fast and produce a flat spectrum that extends to the MHz range, but the ions travel much more slowly and only contribute to frequency components below about 10 kHz. This results in two plateaus with the transition between them at around 10 kHz as shown in Figure 1. The low-frequency plateau is known as the total charge region and the high-frequency plateau as the electron region. Clearly it is important to know what part of the curve the instrumentation is measuring. This is not reflected in Equation 1 because it is a simplification and does not take the pulse shapes into account.

Figure 1: Idealised Campbell spectrum (on logarithmic scale) with diagnostic notes

For neutron flux measurements to be reliable, the signal needs to be bandwidth limited to a stable portion of the spectrum. The Campbell signal is then the mean square current over a set bandwidth. The units of the measurement are therefore A²Hz^-1. For in-core chambers, the A²Hz^-1 measurement is proportional to reactor thermal power. If the fission chamber that produced the results in Figure 1 had a sensitivity of 1x10^-27 A²Hz^-1/nv at 200 kHz, and as flux = signal/sensitivity, then the neutron flux was 10¹⁰ nv.

Campbell mode instruments are usually bandwidth-limited with a centre frequency chosen to be on the electron only part of the spectrum (at say 200 kHz). Choosing a centre frequency near the transition from total charge to electron would be undesirable. The transition frequency varies with ion mobility and polarising voltage. The total charge region is not normally used because a very long averaging time-constant would be required, leading to a slow response time.

Features of the Campbell spectrum

The requirement to square the signal makes the Campbell measurement particularly sensitive to changes in the characteristics of the fission chamber. It is therefore important to periodically test the chambers, particularly if they perform a safety-critical function. Depending on the application and environment, it is recommended that fission chambers should be tested at least annually.

The signal from a fission chamber not only contains information about the neutron flux, it also contains information about some important characteristics of the chamber itself. The transition frequency provides an indication of the gas pressure within the chamber. A reduction in pressure causes the transition frequency to increase. This is because the mobility of the ions increases. The transition frequency also increases with polarising voltage. A reduction in voltage causes the transition frequency to decrease and the sensitivity to fall. Operating the chamber at a correct and stable voltage is therefore very important in Campbell mode.

The appearance of impurities in the fill gas can cause electron capture ionization [6]. This results in the electron plateau reducing in amplitude. However, the total charge plateau amplitude tends to stay the same because the atom that captures the electron becomes a negative ion. This means that the ratio of the amplitudes of the two plateaus gives an indication of gas purity. In reactor flux instrumentation, the development of electron capture is an unsafe condition because it leads to an underestimate of reactor power, based on the incorrect assumption of flux measurement on the electron plateau.

Regular testing allows trends to be identified. This can enable informed decisions to be made about when to replace detectors. Reactor fission chambers can be tested while they are installed. With the reactor producing a known steady flux, the polarising supply is applied to the chamber and measurements taken at various frequency points on a logarithmic scale.

Campbell mode test equipment

A standard spectrum analyser is not ideal for plotting a Campbell spectrum. A spectrum analyser is incapable of polarising the detector, usually has its input impedance fixed at 50 O, and displays results in inappropriate units that require manual conversion. High-temperature fission chambers have integral mineral insulated cables that are usually 33 O. For accurate results, matched impedances are required. For these reasons, a purpose-made instrument has been developed. The signal analyser is effectively a Campbell instrument which has the capability for the pass-band centre-frequency to be varied over a wide range.

A manual signal analyser was developed for Centronic and UKAEA (now Ultra Electronics) around 1980 for use in the UK’s advanced gas-cooled reactors. In that NA3 model, frequency had to be selected manually with range and sweep controls.

UK-based Cooknell Electronics has now developed a new model to replace the 30-year-old devices still in use. It also responded to a perceived need for such an instrument to be made more widely available.

Figure 3: Comparison between the old NA3 and new NA4 output using a noise source as a proxy fission chamber

Figure 3 is a comparison of measurements from the old (NA3) and new (NA4) signal analysers using a current noise source as a proxy fission chamber. The signal source consisted of a 36-stage linear feedback shift register clocked at 100 MHz (which has a reasonably flat spectrum up to 10 MHz). This was connected to the signal analyser via an attenuator and a series 10 kO resistor to turn it into a current source. As Fig. 3 shows, apart from some roll-off below 2 kHz, they are in good agreement. At least some of this roll-off is caused by the 10 kO source resistance interacting with the polarising voltage blocking capacitor in the signal analyser. With a real fission chamber this would not occur.

A conventional Campbell instrument (such as a reactor protection instrument) that is being used with a fission chamber will have a measurement bandwidth and centre frequency. If the signal analyser is used to measure the spectra at the same polarising voltage as that instrument, the suitability of the chamber and polarising voltage can be seen. If the transition frequency of the spectrum lies within the measurement band of the protection instrument, there is a problem. The system would be very sensitive to changes in detector gas and polarising voltage. If the instrument is measuring in the electron region, signs of electron capture need to be looked for. If the instrument is measuring in the total charge region, the measurement is insensitive to electron capture. However, this region has the disadvantage of requiring a longer averaging time-constant due to the low frequencies being measured. Hence, either the reading from the instrument will be very noisy, or the response time will be very slow. Incidentally, fission chambers are used in Campbell mode for fusion reactors, not just fission reactors. The response time must be very fast (1ms), so the pass band has to be centred on the electron region. Future Campbell flux instruments are likely to have digital processing, but knowing about the spectra produced by the chamber is still of fundamental importance.

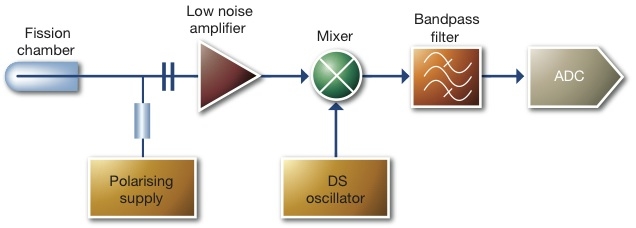
A block diagram of signal analyser electronics design is shown in Figure 4.

Figure 4 : Signal analyser electronics design block diagram

A low-noise variable power supply provides up to 1000 V to polarise the fission chamber. The ac component of the signal is coupled to an amplifier which has an input impedance switchable between 33 O, 50 O and 75 O to suit most chamber cables. A low-noise amplifier is used, giving a noise floor of

6x10^-23 A²Hz^-1 with no chamber or cable connected. To avoid difficulties associated with sweeping a high-order filter over a wide range, an approach similar to a superheterodyne receiver has been taken. The output of the amplifier is mixed with the output of a Direct Digital Synthesis (DDS) oscillator. The DDS oscillator can be accurately varied from 1 kHz to 60 MHz under microprocessor control. The output of the mixer is fed to an eighth-order band-pass filter centred on 200 Hz with a 50 Hz bandwidth. A mixer generates output frequencies that are the sum and difference of the input frequencies. Hence two 50 Hz bands of the input signal, 200 Hz either side of the DDS oscillator frequency, are shifted to the pass band of the filter. Sweeping the oscillator is therefore equivalent to sweeping a filter with a 100 Hz bandwidth. The double sideband type response is acceptable because of the smooth variation of the Campbell spectrum. The filter output is digitised by a delta-sigma analogue-to-digital converter. The squaring and averaging is then carried out in software, as is auto-ranging by switching the gain of the pre-amplifier. The averaging time is variable and an alternative 500 Hz filter (giving an effective bandwidth of 1 kHz) can be selected, enabling a faster sweep.

This article was first published in the December 2011 issue of Nuclear Engineering International magazine.

Robert Hunt, Cooknell Electronics Ltd, 17 Cambridge Road, Granby Industrial Estate, Weymouth, Dorset DT4 9TJ, United Kingdom