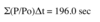Fukushima Daiichi crisis
Simplified Modeling of the Reactor Primary System and Containment Response following Reactor Scram
10 October 2011This document describes the simplified models used to predict the reactor primary system and containment response following scram. By James Healzer
For this analysis, a BWR 4 with 764 fuel bundles, operating at a thermal power of 3293 MW has been used. The reactor is assumed to be in a Mark I containment. Of interest in this study is the approximate time after scram until the core starts to uncover and the containment wetwell response, that is the pressure and suppression pool temperature. The sequence of events for the case that is examined is that after reactor scram, the reactor core isolation cooling system (RCIC) operates, but only for 4 hours. The RCIC removes steam from the primary system, holding the primary system near its 1050 design pressure. The steam is condensed in the suppression pool and water from the suppression pool is returned to the pressure vessel, maintaining its water inventory. During this period, the suppression pool will heat up, increasing the suppression pool air space pressure, but the core will remain covered. After 4 hours, the RCIC is assumed to stop operation, and the pressure vessel will pressurize to the SRV set point and they will cycle open and closed, dumping steam from the pressure vessel to the suppression pool, until the core begins to uncover. This case estimates the time for this to occur, assuming 4 hours of RCIC operation.
1. From the attached decay heat table (Table 1), the relative reactor power level and integrated decay heat dump after 4 hours will be:
P/Po = 0.0102 and

2. The decay heat dump to the RPV for the case chosen here will then be:
Power = (196.0sec)(3.111x106BTUs/sec) = 6.1x108 BTUs
3. The suppression pool temperature rise due to this energy addition will become:
Pool delta T = (6.1x108 BTUs)/ (122470ft3)(62lbm/ft3)(1.0°F/BTU) = 80.3°F
4. Assuming the air space will remain in thermal equilibrium with the pool, the pressure will become:
p/po = (T/To) = (100+460+80.3)/(100+460) = 1.143 then p = 1.143(19.0) = 21.7 psia
After 4 hours, and the RCIC no longer operates, the core power will be reduced to approximately 1% of its rated value, but the liquid in the RPV will remain the same, since all liquid boiled off was replaced by the RCIC. To estimate the time for this inventory to boil off so the water level reaches the top of the core, the liquid inventory is estimated. It is assumed at 4 hours and the low power level, the void fraction in the core is nearly zero. Using the reactor vessel volumes in the attached table (Table 2, from EPRI NP-2856-CCM):
5. Liquid volume outside shroud = 1631(1-0.047)+2690(41.5-31.79)/(41.5-26.49) = 3307.0 ft3
6. Liquid volume inside shroud = 1376(1-0.610) + 369(1-0.674) – 969(0.369) = 299.3 ft3
7. Total liquid volume over core = 3307.0 + 299.3 = 3606.3 ft3
8. Energy = (3606.3)(44.4)(602.2) = 9.64x107 BTUs
9. With a decay heat fraction of 0.01, the time for boil-off to the top of the core becomes:
t = 9.64x107/(0.01)( 3.111x106) = 3100 sec = 0.86 hr
The associated suppression pool temperature and air space pressure rise will be:
10. Pool delta T = (9.64x107 BTUs)/ (122470ft3)(62lbm/ft3)(1.0°F/BTU) = 12.9°F
11. p/po = (T/To) = (100+80.3+12,7+460)/(100+80.3+460) = 1.02, then p = 1.02(21.7) = 22.1 psia
In summary, for this case with 4 hours of RHR operation, the time after scram for the water level in the RVP to reach the top of the core was approximated to be:
t (top of core) = 4 + 0.86 = 4.86 hours
The associated suppression pool temperature rise, starting from 100°F and air space pressure, starting from 19 psia was approximated to be:
12. Tpool = 100 + 80.3 + 12.9 = 193.2°F
13. p(air space) = 22.1 psia
Since the RCIC puts back everything it takes out, the liquid inventory to be boiled off before the core uncovers will be about the same as for the case where the RCIC does not operate. With the RCIC the core voids essentially go to zero after 4 hours, so it takes some inventory to fill the core, but for no RCIC, we have a little more inventory to boil off. For this case, the reactor pressurizes up to the SRV set-point and the SRVs cycle, holding the pressure at the set-point and dumping steam to the suppression pool. The difference is that with the RCIC, the decay heat level is down to 1% when it shuts down, so the boil off to the top of the core is 0.8 hours. In the case with no RCIC, the boil-off starts at the beginning of the decay heat curve. Using the decay heat table (Table 1), the boil off occurs in approximately 1200 sec, or in about 20 minutes. In this case, if the operator has no high pressure make-up, and only low pressure make-up in the feedwater attachment, he has only approximately 20 minutes to activate ADS, and get the low pressure system in operation, to avoid core uncovery and potential damage.
A more extensive calculation of Peach Bottom with the computer code MELCORE is provided in NUREG/CR 5850 assuming station blackout and no automatic depressurization (which is not justified). That report assumes 5 hours of RCIC operation and predicts zircaloy oxidation after 76 minutes from the time of core uncovery and melt and relocation after close to two hours. Those results confirm the urgency to add water to the reactor as predicted by this simplified approach.
TablesTable 1: ANS – 5 Decay Heat Curve, Infinite Exposure, Infinite Irradiation Table 2A: Suppression chamber Table 2B: Reactor Table 2C: Vessel inventory summary Table 2D: Reactor elevations